Pertidaksamaan Eksponen dan Sifat-Sifatnya
Pertidaksamaan Eksponen dan Sifat - Sifatnya
Pertidaksamaan eksponen adalah pertidaksamaan jenis eksponen yang memiliki variabel. Dalam bentuk pertidaksamaan, sifat-sifat pertidaksamaan eksponen dapat diketahui sebagai berikut:


Intinya, kalau basisnya > 1, maka tanda pertidaksamaannya tetap. Sebaliknya, kalau basisnya pecahan (0<basis>1), maka tanda pertidaksamaannya berubah, misalnya dari "<" jadi ">", atau "≤" jadi "≥", atau sebaliknya.
- Untuk 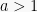
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Untuk 
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Bentuk eksponen harus diuraikan sampai diperoleh bentuk yang sama. Uraikan berdasarkan sifat-sifat eksponen.
- Gunakan permisalan bentuk eksponen dengan variabel tertentu.
- Selesaikan pertidaksamaannya menggunakan konsep pertidaksamaan sampai diperoleh interval untuk permisalannya.
- Susbtitusikan nilai balik yang diperoleh pada permisalan.
Naila Zia Khalishah
X MIPA 2
No. Absen 27



Komentar
Posting Komentar