_-_MATEMATIKA_12_-_SEGITIGA-03.png?width=820&name=SEPARATOR_(2)_-_MATEMATIKA_12_-_SEGITIGA-03.png)
Dalil Titik Tengah dan Dalil Intersept pada Segitiga Masalah Geometri Beserta Contoh Soalnya
Dalil (teorema) merupakan kebenaran yang diturunkan dari suatu aksioma. Kebenaran ini perlu dibuktikan, jadi tidak hanya berupa pernyataan saja. Nah, aksioma sendiri adalah suatu pernyataan yang dijadikan pedoman dasar, sehingga tidak memerlukan pembuktian.
Dalil Titik Tengah Segitiga
Dalil titik tengah segitiga berbunyi:
“Ruas garis yang menghubungkan titik-titik tengah pada dua sisi segitiga akan sejajar dengan sisi ketiga segitiga. Panjang ruas garis tersebut adalah setengah dari panjang sisi ketiga segitiga”.
atau
"Segmen garis penghubung titik-titik tengah dari kedua sisi segitiga adalah sejajar dengan sisi ketiga dan panjangnya adalah setengah kali panjang sisi ketiga tersebut."
Jika kamu perhatikan gambar di bawah, titik E adalah titik tengah sisi AB dan titik D adalah titik tengah sisi AC. Sehingga, terbentuklah ruas garis ED. Nah, garis ED ini akan sejajar dengan garis BC dan kita dapat menghitung panjang ED, yaitu ED = ½ BC.
Dalil Intersept (Intercept)
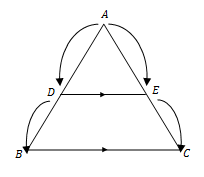
"Jika sebuah garis sejajar dengan salah satu sisi sebuah segitiga ABC (misal garis tersebut sejajar sisi BC) dan memotong dua sisi lain dari segitiga tersebut (yaitu sisi AB dan AC) di titik D dan E, maka berlaku persamaaan kesebandingan sebagai berikut :"
atau
Jika dua atau lebih garis sejajar dipotong oleh dua garis berpotongan, maka rasio dari ruas garis berpotongan pertama adalah sama dengan rasio dari ruas garis yang serupa dari garis perpotongan kedua.
Jadi, pada segitiga ABC di atas, terdapat garis DE yang sejajar dengan AB, dan kemudian garis-garis sejajar itu dipotong oleh dua garis yang berpotongan yakni CA dan CB, maka berlaku:

Pengembangan dari dalil ini, apabila terdapat tiga garis sejajar dan ketiga garis itu dipotong oleh dua garis yang berpotongan, seperti tampak pada gambar di samping, maka berlaku perbandingan:


Contoh Soal :
1. Sebuah palang berbentuk segitiga sama kaki. Alas dan sebuah kakinya memiliki perbandingan 2 : 3 dengan tinggi segitiga 16 cm. Hitung luas segitiga tersebut!
A. 61√5
B. 63√2
C. 65√1
D. 64√2
E. 62√3
Jawaban : D
Pembahasan :
Pada segitiga siku-siku, berlaku Teorema Pythagoras, sehingga diperoleh hasil sebagai berikut :
Dengan demikian, panjang alas segitiga adalah
2a = 2(4√2) = 8√2 cm
Jadi, luas segitiga tersebut adalah
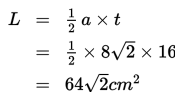
2. Perhatikan gambar segitiga PQR di bawah ini:
Jika panjang ruas garis ST = 15 cm, berapakah panjang ruas garis QR
A. 28 cm
B. 30 cm
C. 34 cm
D. 36 cm
E. 42 cm
Jawaban : B
Pembahasan :
Karena titik S merupakan titik tengah ruas garis QP dan titik T titik tengah ruas garis PR, maka berlaku dalil titik tengah sehingga diperoleh:
ST = 1/2 x QR
QR = 2 x ST
QR = 2 x 15 = 30 cm
3. Perhatikan segitiga ABC siku-siku di B pada gambar di bawah ini:
Jika panjang BE = 5 cm dan panjang AD = 13 cm, berapakah panjang AB dan DE?
A. 3
B. 7
C. 6
D. 9
E. 5
Jawaban : C
Pembahasan :
BC = 2 x BE = 2 x 5 = 10
AC = 2 x AD = 2 x 13 = 26
Dengan menggunakan teorema pythagoras, kita peroleh:
AB² = AC² - BC²
AB² = (AC + BC)(AC - BC)
AB² = (13 + 5)(13 - 5)
AB² = 18 x 8
AB² = 144
AB = √144
AB = 12
Dengan menggunakan dalil titik tengah pada segitiga kita peroleh :
DE = 1/2 x AB = 1/2 x 12 = 6
4. Perhatikan gambar berikut
Nilai x + y pada gambar adalah....
A. 44
B. 34
C. 52
D. 21
E. 12
Jawaban : A
Pembahasan :
Perhatikan segitiga CDE, berdasarkan dalil titik tengah pada segitiga, maka kita peroleh:
x = 1/2 x DE = 1/2 x 22 = 11
Segitiga ABC sebangun dengan segitiga CDE, maka berlaku:
AC/DC = AB/DE
3/2 = y/22
y = 3/2 x 22
y = 33
Maka x + y = 11 + 33 = 44
5. AD : BD = 3 : 2 dan AB = 12 cm, tentukan 7,2 panjang DE!
A. 5 cm
B. 7 cm
C. 6 cm
D. 9 cm
E. 2 cm
Jawaban : C
Pembahasan :
AD = X 12 = = 7,2
Menurut dalil intercept segitiga diperoleh
AD : AB = DE : BC
7,2 : 12 = DE : 10
12 x DE = 7,2 x 10
DE = = 6 cm
Jadi, panjang DE adalah 6 cm
X MIPA 2 // 28
Daftar Pustaka :Matematika Kelas 12 | Garis Istimewa dan Dalil yang Berkaitan Pada Segitiga
Geometri bidang datar dan dalil dalil pada segitigahttps://www.materimatematika.com/2017/11/dalil-segmen-garis.html?m=1 https://www.danlajanto.com/2016/02/penerapan-sifat-sifat-geometri-bidang.html?m=1 https://jegeristik.blogspot.com/2017/04/contoh-soal-pemecahan-masalah-nyata.html?m=1
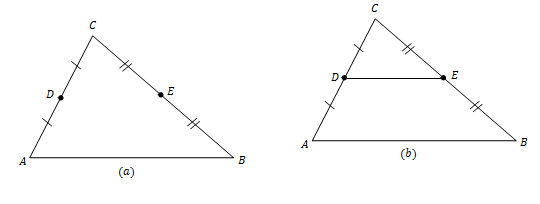
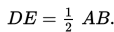
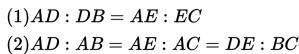

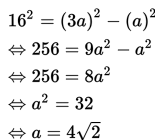
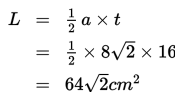
_-_MATEMATIKA_12_-_SEGITIGA-03.png?width=820&name=SEPARATOR_(2)_-_MATEMATIKA_12_-_SEGITIGA-03.png)











Komentar
Posting Komentar