Proyeksi Ortogonal dan Panjang Proyeksi beserta Contoh Soalnya

Proyeksi Ortogonal Dan Panjang Proyeksi

Proyeksi merupakan ilmu yang mempelajari tentang cara pandang objek dalam ruang dimensi tiga dalam gambar di ruang dimensi dua. Cara ini mempermudah kita untuk melihat objek yang terletak di ruang dimensi tiga. Pada proyeksi vektor, objek yang diproyeksikan berupa vektor, baik itu panjangnya atau vektor itu sendiri. Proyeksi dibedakan menjadi beberapa jenis, di antaranya adalah proyeksi ortogonal, aksonometri, proyeksi miring (oblique), dan perspektif. Pada pembahasan proyeksi vektor kali ini hanya akan membahas mengenai proyeksi vektor ortogonal. Jadi, untuk jenis proyeksi lainnya tidak akan dibahas pada halaman ini.

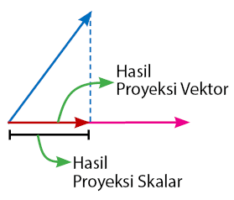
Proyeksi ortogonal adalah cara pandang mata pada sebuah objek yang ditarik garis tegak lurus pada sebuah bidang datar. Terdapat dua proyeksi ortogonal yang akan di bahas pada pembahasan kali ini, yaitu proyeksi skalar dan vektor ortogonal. Perhatikan gambar dua proyeksi vektor dengan arah yang berbeda pada gambar di bawah

Proyeksi Skalar dan Proyeksi Vektor Ortogonal

Proyeksi Skalar Ortogonal

Proyeksi skalar ortogonal biasa disebut juga dengan proyeksi panjang vektor ortogonal. Dalam kata lainnya, objek proyeksi adalah panjang vektor. Rumus untuk menghitung panjang proyeksi skalar vektor ortogonal adalah sebagai berikut.

Proyeksi skalar ortogonal $\vec{a}$ pada arah vektor $\vec{b}$ .
$\left| \vec{c} \right| = \frac{\vec{a} \cdot \vec{b}}{ \left| \vec{b} \right| }$
Proyeksi skalar ortogonal $\vec{b}$ pada arah vektor $\vec{a}$ .
$\left| \vec{c} \right| = \frac{\vec{a} \cdot \vec{b}}{ \left| \vec{a} \right| }$

Proyeksi Vektor Ortogonal

Objek pada proyeksi skalar vektor ortogonal adalah panjang proyeksi vektor. Sedangkan pada proyeksi vektor ortogonal yang menjadi objek utamanya adalah vektornya. Vektor hasil proyeksi dapat ditentukan melalui rumus berikut.

Proyeksi vektor ortogonal $\vec{a}$ pada $\vec{b}$ .
$\vec{c} = \frac{\vec{a} \cdot \vec{b} }{\left| \vec{b} \right| ^{2} } \cdot \vec{b}$
Proyeksi vektor ortogonal $\vec{b}$ pada $\vec{a}$ .
$\vec{c} = \frac{\vec{a} \cdot \vec{b} }{\left| \vec{a} \right| ^{2} } \cdot \vec{a}$

Panjang Proyeksi Vektor

Misalkan OA = a, OB = b, dan OP = p, dengan |a| , |b| dan |p| berturut-turut adalah panjang dari vektor a, b dan p.

Dengan bantuan trigonometri, panjang proyeksi vektor a pada b, yaitu |p| dapat dinyatakan dalam bentuk :
|p| = |a| cos θ, jika θ lancip
|p| = -|a| cos θ, jika θ tumpul

Mengingat

\begin{aligned} c o s θ = \frac{a \cdot b}{| a | | b |} \end{aligned}

, maka

\begin{aligned} | p | & = | a | \frac{a \cdot b}{| a | | b |} = \frac{a \cdot b}{| b |}, θ l a n c i p \end{aligned}

\begin{aligned} | p | & = - | a | \frac{a \cdot b}{| a | | b |} = - \frac{a \cdot b}{| b |}, θ t u m p u l \end{aligned}

Walaupun persamaan terakhir bertanda negatif, namun nilainya tetap positif. Hal ini disebabkan, ketika θ tumpul, maka a ‧ b < 0.

Secara umum, panjang proyeksi vektor a pada b, yaitu |p| kita rumuskan

$\begin{aligned} | p | = \frac{| a \cdot b |}{| b |} \end{aligned}$

dengan
|p| = panjang proyeksi vektor a pada b
|b| = panjang b
|a ‧ b| = nilai mutlak dari a ‧ b

Proyeksi Skalar

Proyeksi skalar a pada b adalah suatu skalar yang nilainya sama dengan panjang proyeksi vektor a pada b, namun bertanda negatif jika vektor proyeksinya berlawanan arah dengan b.

Apabila proyeksi skalar a pada b kita notasikan dengan s, maka

$\begin{matrix} s = \frac{a \cdot b}{| b |} \end{matrix}$

Contoh Soal :

1.) Panjang proyeksi ortogonal vektor $\vec{a} = (p, 2, 4)$ pada $\vec{b} = (2, p, 1)$ adalah 4. Nilai p adalah ….

$\textrm{A.} \; \; \; -4$

$\textrm{B.} \; \; \; -2$

$\textrm{C.} \; \; \; - \frac{1}{2}$

$\textrm{D.} \; \; \; \frac{1}{2}$

$\textrm{E.} \; \; \; 2$

Jawaban : E

Pembahasan :

Mencari panjang vektor b:

$\left| \vec{b} \right| = \sqrt{2^{2} + p ^{2} + 1^{2}}$

$\left| \vec{b} \right| = \sqrt{4+ p ^{2} + 1}$

$\left| \vec{b} \right| = \sqrt{p ^{2} + 5}$

Berdasarkan rumus proyeksi skalar (proyeksi panjang) ortogonal vektor dapat diperoleh persamaan berikut.

$\left| \vec{c} \right| = \frac{\vec{a} \cdot \vec{b}}{\left| \vec{b} \right|}$

$4 = \frac{(p, 2, 4)(2, p, 1)}{\sqrt{p^{2}+5}}$

$4 = \frac{2p + 2p + 4}{\sqrt{p^{2}+5}}$

$4 = \frac{4p + 4}{\sqrt{p^{2}+5}}$

$4 = \frac{4(p + 1)}{\sqrt{p^{2}+5}}$

$1 = \frac{p + 1}{\sqrt{p^{2}+5}}$

$\sqrt{p^{2}+5} = p + 1$

$p^{2}+5 = (p + 1)^{2}$

$p^{2}+5 = p^{2} + 2p + 1$

$5 = 2p + 1$

$2p = 5 - 1$

$2p = 4 \rightarrow p=\frac{4}{2} = 2$

2.) Diketahui a = [8, 4] dan b = [4, -3]. Tentukan panjang proyeksi vektor a pada b dan panjang proyeksi vektor b pada a ...

A. √5

B. 3√2

C. √3

D. 5√3

E. √2

Jawaban : A

Pembahasan :

Panjang proyeksi vektor a pada b adalah

\begin{aligned} | p | = \frac{| a \cdot b |}{| b |} = \frac{| 8 (4) + 4 (- 3) |}{\sqrt{4^{2} + (- 3)^{2}}} = \frac{| 20 |}{5} = 4 \end{aligned}

Panjang proyeksi vektor b pada a adalah

\begin{aligned} | p | = \frac{| a \cdot b |}{| a |} = \frac{| 8 (4) + 4 (- 3) |}{\sqrt{8^{2} + 4^{2}}} = \frac{| 20 |}{\sqrt{80}} = \sqrt{5} \end{aligned}

3.) Panjang proyeksi vektor a = 3i + 4j - k pada vektor b = i - 2j + k adalah ...

A. √11

B. √6

C. √3

D. 6

E. 2√3

Jawaban : B

Pembahasan :

a = [3, 4, -1]
b = [1, -2, 1]

Panjang proyeksi vektor a pada b adalah

\begin{aligned} | p | = \frac{| 3 (1) + 4 (- 2) + (- 1) 1 |}{\sqrt{1^{2} + (- 2)^{2} + 1^{2}}} = \frac{| - 6 |}{\sqrt{6}} = \sqrt{6} \end{aligned}

4.) Diketahui vektor u = i + 2j - 3 k dan v = 2i - 3j - 6 k. Proyeksi skalar dari u pada v adalah...

A. 1

B. 2
C. 3
D. 4
E. 5

Jawaban : B

Pembahasan :
Hitung terlebih dahulu |v|
|v| = √(22 + (- 3)2 + (- 6)2) = √4 + 9 + 36 = √49 = 7
Menghitung u . v
u . v = 1 . 2 + 2 . - 3 + - 3 . - 6 = 2 - 6 + 18 = 14
Maka proyeksi skalar u pada v = u . v / |v| = 14 / 7 = 2

5.) Diketahui vektor u = i + 2j - 3 k dan v = 2i - 3j - 6 k. Proyeksi vektor u pada v adalah...

A. 4i + 6j - 12k
B. 4i - 6j + 12k
C. 4i - 6j - 12k
D. 4i + 6j + 12k
E. 2i - 3j - 6k

Jawaban : C

Pembahasan :
Hitung terlebih dahulu |v|
|v| = √(22 + (- 3)2 + (- 6)2) = √4 + 9 + 36 = √49 = 7
Menghitung u . v
u . v = 1 . 2 + 2 . - 3 + - 3 . - 6 = 2 - 6 + 18 = 14
Proyeksi vektor u pada v = (u . v) v / |v|2 = 14 / 7 v = 2 (2i - 3j - 6k) = 4i - 6j - 12k

6.) Diketahui vektor u = i + 2j - 3 k dan v = 2i - mj - 6 k. Jika panjang proyeksi u pada v sama dengan 1/2 panjang v, maka salah satu proyeksi vektor u pada v adalah....

A. 20/49 i - 120/49 k
B. 20/49 i + 120/49 k
C. 20/7 i - 120/49 k
D. 20/49 i - 120/7 k
E. 20/7 i - 120/7 k

Jawaban : A

Pembahasan
Hitung terlebih dahulu |v|
|v| = √(22 + (- 3)2 + (- 6)2) = √4 + 9 + 36 = √49 = 7
u . v / |v| = 1/2 |v|
2 . u . v = |v|2
2 (1 . 2 - 2 . m + (- 3 . - 6) = (√22 + (-m)2 + (-6)2)2
2 (2 - 2m + 18) = 4 + m2 + 36
4 - 4m + 36 = 40 + m2
m2 + 4m + 40 - 40 = 0
m2 + 4m = 0
m = 0 atau m = - 4
Jika m = 0 maka v = 2i - 6k
Jika m = - 4 maka v = 2i - 4j - 6k

Untuk v = 2i - 6k, maka proyeksi vektor u pada v

= (u . v) v / |v|2

= (1 . 2 + 2 . 0 + (- 3 . - 6)) (2i - 6k) / 49

= 20 (2i - 6k) / 49

= 20i - 120k / 49

= 20/49 i - 120/49 k

Untuk v = 2i - 4j - 6k, proyeksi vektor u pada v

= (u . v) v / |v|2

= (1 . 2 + 2 . -4 + (- 3 . - 6)) (2i - 4j - 6k) / 49

= 12 (2i - 4j - 6k) / 49

= 24i - 48 j - 72k / 49

= 24/49 i - 48/49 j - 72/49 k

7.) Diketahui vektor-vektor sebagai berikut:

Contoh soal proyeksi skalar berbentuk matriks

Proyeksi skalar a pada (b + c) adalah....
A. 2/5
B. 3/5
C. 4/5
D. 7/5
E. 9/5

Jawaban : A

Pembahasan
Hitung terlebih dahulu b + c

Menghitung |b + c|
|b + c| = √(-4)2 + (3)2 + 02 = √16 + 9 = 5

Menghitung a . (b + c)
a . (b + c) = (1 . -4) + (2 . 3) + 3 . 0 = 2

Maka proyeksi skalar a pada (b + c)

= a . (b + c) / |b + c|

= 2/5

8.) Diketahui A(1, 2, 3), B(2, 3, 4) dan C(3, 4, 5). Jika AC mewakili a dan AB mewakili b maka nilai dari |a|, |b| dan a . b berturut-turut adalah...

A. √3, 2√3, 6
B. √3, √3, 6
C. √3. √3, √3
D. √3, √3, √6
E. √6, √6, √6

Jawaban : A

Pembahasan
a = AC = C - A = (3, 4, 5) - (1, 2, 3) = (2, 2, 2)
b = AB = B - A = (2, 3, 4) - (1, 2, 3) = (1, 1, 1)

Sehingga
|a| = √(1)2 + (1)2 + (1)2 = √3
|b| = √(2)2 + (2)2 + (2)2 = √12 = 2√3
a . b = (1, 1, 1) . (2, 2, 2) = 2 + 2 + 2 = 6

Daftar Pustaka :

https://idschool.net/sma/proyeksi-skalar-dan-proyeksi-vektor-orthogonal/

https://smatika.blogspot.com/2018/09/proyeksi-skalar-dan-proyeksi-vektor.html

http://barugurukita.blogspot.com/2016/08/pembahasan-contoh-soal-proyeksi.html

Naila Zia Khalishah

X MIPA 2

No. Absen 28

Cari Blog Ini

NAILA ZIA KHALISHAH