Vektor, Jenis Vektor, Operasi Vektor, dan Contoh Soalnya
Vektor adalah besaran yang mempunyai besar/nilai dan arah. Secara geometris vektor digambarkan sebagai ruas garis berarah, dengan panjang ruas garis menyatakan besar vektor dan arah ruas garis menyatakan arah vektor .
Dalam matematika vektor digambarkan dalam bentuk garis lurus yang mempunyai panjang dan arah.
Misalkan vektor merupakan vektor yang berawal dari titik
menuju titik
dapat digambarkan koordinat cartesius dibawah. Panjang garis sejajar sumbu x adalah
dan panjang garis sejajar sumbu y adalah
merupakan komponen-komponen vektor
.

Komponen vektor dapat ditulis untuk menyatakan vektor secara aljabar yaitu:
atau
- dengan menggunakan huruf kapital harus menggunakan dua huruf, sebagai contoh vektor AB⃗
- adalah vektor yang panjangnya sama dengan panjang ruas garis AB dan arahnya dari A ke B.
- sedangkan dengan huruf kecil hanya satu huruf, sebagai contoh a̅
- Vektor Nol adalah vektor yang besarnya nol satuan dan arahnya tak tertentu.
- Vektor Posisi adalah Posisi sebuah titik partikel terhadap sebuah titik acuan tertentu dapat dinyatakan dengan sebuah vektor posisi.

- Vektor Basis adalah vektor yang panjangnya satu satuan dan arahnya searah dengan sumbu koordinat.
Secara aljabar sebuah vektor dapat dinyatakan dengan salah satu cara, sebagai berikut :
Contoh Soal Vektor Kolom, Baris dan Basis Dan Jawabannya
Modulus Vektor ( Panjang Vektor )
Jika A (x A , y A , z A ) dan B (x B , y B , z B ) maka panjang vektor OA adalah OA atau a , yaitu :
Pembagian Ruas Garis Vektor
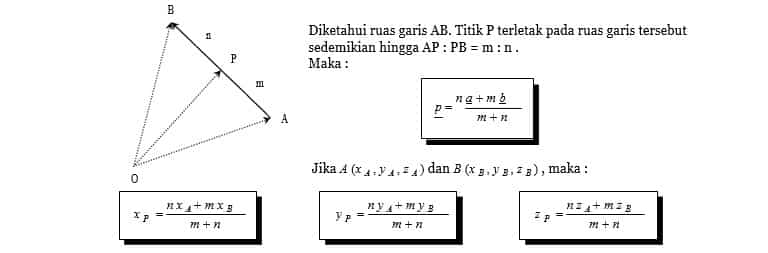
Diketahui ruas garis AB. Titik P terletak pada ruas garis tersebut sedemikian hingga AP : PB = m : n . Maka :
Pada perbandingan AP : PB = m : n ,
- Jika P terletak di antara A dan B , maka m > 0 dan n > 0 .
- Jika P terletak pada perpanjangan AB , maka m < 0 dan n > 0 .
- Jika P terletak pada perpanjangan BA , maka m > 0 dan n < 0 .
1. Perkalian Vektor Dengan Bilangan Riil
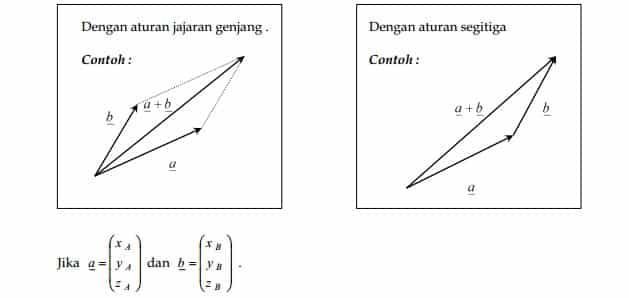
Diketahui vektor a dan b .
Secara geometris vektor a dan b dapat dijumlahkan dengan cara sebagai berikut :
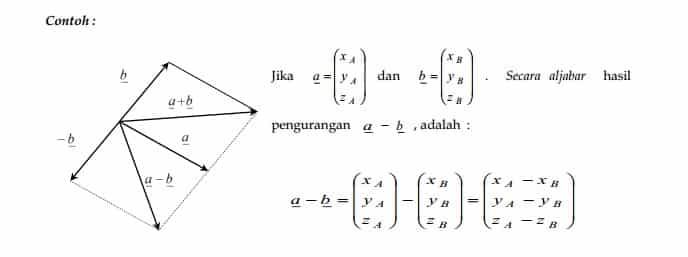
3. Pengurangan Vektor
Diketahui vektor a dan b . Pengurangan vektor a – b dapat dinyatakan dalam bentuk penjumlahan vektor a + ( – b ) , dengan vektor – b adalah vektor yang panjangnya sama dengan vektor b dan arahnya berlawanan dengan vektor b .
Contoh Soal
Pilihan Ganda
Nomor 1
Diketahui a = t i - 8 j + h k dan b = (t +2) i + 4 j + 2 k. Jika a = - b maka vektor a dapat dinyatakan ...A. i + 8j + 2 k
B. i + 8 j - 2k
C. i - 8j + 2k
D. - i - 8j + 2k
E. - i - 8j - 2k
Pembahasan
a = - b maka t i - 8 j + h k = - (t +2) i - 4 j - 2 k
t = - (t +2)
t = - t - 2
2t = -2
t = -1
lalu h = -2
sehingga, a = - i - 8 j - 2 k
Jawaban: E
Nomor 2
Jika vektor a = 10i + 6 j - 3k dan b = 8 i + 3 j + 3k serta c = a - b, maka vektor satuan yang searah denga c adalah...
A. 6/7 i + 2/7 j + 3/7 k
B. 2/7 i + 3/7 j - 6/7 k
C. 2/7 i - 3/7 j + 6/7 k
D. 6/7 i - 3/7 j - 2/j k
E. -2/7 i + 6/7 j - 3/7 k
Pembahasan
c = a - b = (10 i + 6 j - 3k) - (8i + 3 j + 3k) = 2 i + 3j - 6k
Sehingga

Maka vektor yang searah dengan c adalah
c = (2, 3, -6) / 7 atau c = 2/7 i + 3/7 j - 6/7 k
Jawaban: B
Nomor 3
Diketahui titik-titik A (2, 5, 2), B (3, 2, -1), C (2, 2, 2). Jika a = AB dan b = CA dan c = b - a maka vektor c adalah...
A. (1,5,3)
B. (-1,5,3)
C. (-1,0,3)
D. (-1,3,5)
E. (-1,-3,5)
Pembahasan
a = AB = B - A = (3,2,-1) - (2,5,2) = (1,-3,-3)
b = CA = A - C = (2,2,2) - (2,5,2) = (0,-3,0)
c = b - a = (0,-3,0) - (1,-3,-3) = (-1,0,3)
Jawaban:C
Nomor 4
Diketahui U = 3 i + 2 j + k dan v = 2i + j dimana W = 3 U - 4 V maka besar W =...
A. √5
B. √7
C. √11
D. √13
E. √14
Pembahasan
W = 3 (3 i + 2 j + k) - 4 (2i + j) = i + 2j + 3k

Jawaban: E
Nomor 5
Diketahui A (1,2,3), B(3,3,1) dan C(7,5,-3). Jika A, B, dan C segaris, perbandingan AB : BC =...
A. 1 : 2
B. 2 : 1
C. 2 : 5
D. 5 : 7
E. 7 : 5
Pembahasan
AB = B - A = (3,3,1) - (1,2,3) = (2,1,-2)
Besar AB = √22 + 12 + (-2)2 = 3
BC = C - B = (7,5,-3) - (3,3,1) = (4,2,-4)
Besar BC = √42 + 22 + (-4)2 = 6
Jadi perbandingan AB : BC = 3 : 6 = 1 : 2
Jawaban: A
Nomor 6
Jika vektor
maka vektor a + 2b - 3c = ...
Pembahasan

Jawaban: D
Essay
3. Diketahui ada titik A(1, 3, 5), titik B(4, 6, 2), dan titik C(m, n, -5). Apabila titik A, B, dan C segaris maka tentukan nilai p + q !
Penyelesaian :
Jika titik – titik A, B, dan C segaris maka vektor AB dan vektor AC bisa juga searah atau berlainan arah.
Sehingga akan ada bilangan m yang merupakan sebuah kelipatan dan bisa membentuk persamaan berikut ini :

Jika B ada diantara titik A dan C, maka
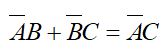
Sehingga
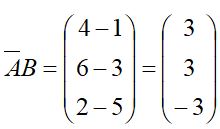

Maka kelipatan m dalam persamaan dapat ditemukan sebagai berikut
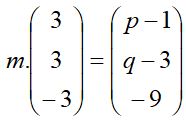
m . (-3) = -9, maka m = 3
Dengan subsitusi nilai m, akan diperoleh:
m . 3 = p – 1, maka p= -8
m . 3 = q – 3, maka q= -6
Jadi,
p + q = – 8 – 6 = – 14
Sumber :
https://www.gurupendidikan.co.id/vektor-matematika/
http://kuncijawaban4.blogspot.com/2017/05/soal-vektor-matematika.html?m=1
Naila Zia Khalishah
X MIPA 2 // 28



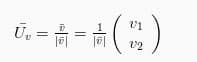
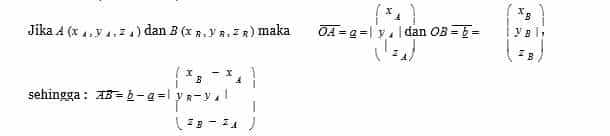
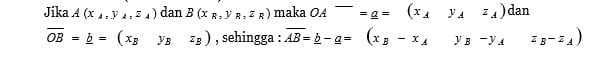
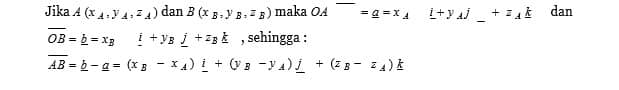







Komentar
Posting Komentar